Leetcode Weekly Breakdown #432

After months of practice I've finally achieved Knight status on Leetcode! (top 25% among players ranked 1600+, ~top 5% sitewide)

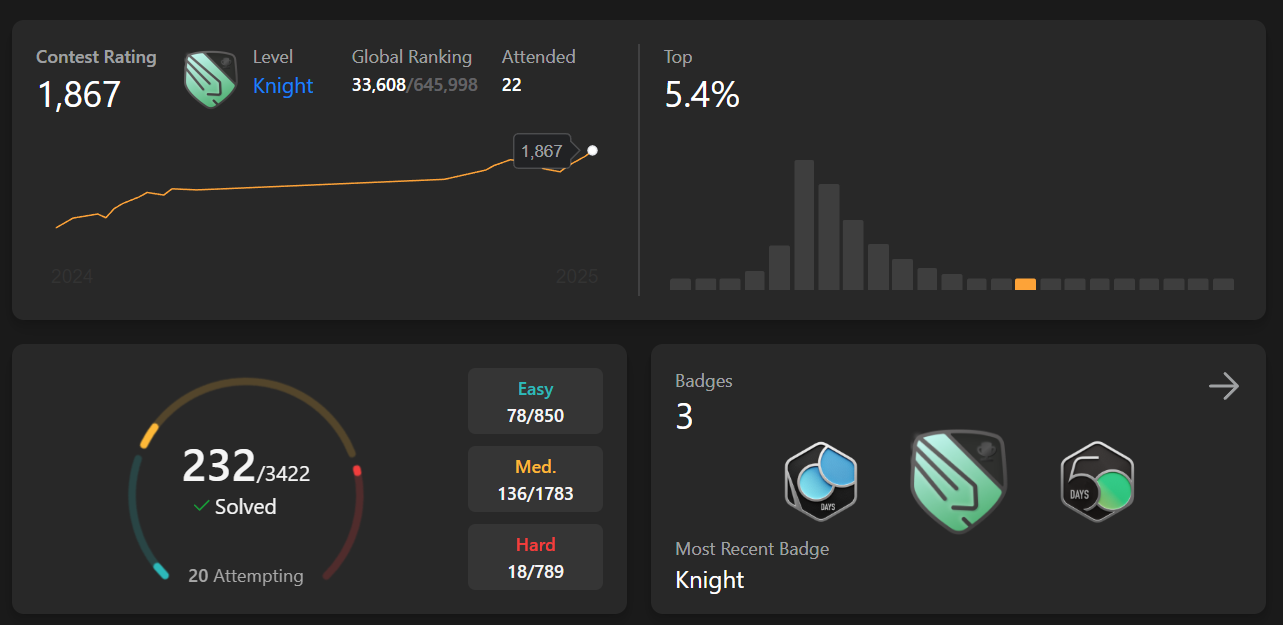
I know it's not much, and I've still got a long way to go, but the badge serves as proof to me that I'm making progress. It also means that I now feel competent enough to share my intuitions, solutions, and thought processes here in the hopes that they might be able to help someone else.

Why you should read this

At this point I'm not good enough to solve all 4 problems; but if you're an aspiring Leetcoder (or an aspiring Knight!) I'm good enough to help you reach your goals. I believe I've crafted explanations that are quick to read and easy to understand - I break my code into 5-10 chunks which are each explained in a few sentences. I also don't edit my submissions before posting them here. What you see is what I wrote during the contest! This means the code isn't the neatest but is reflective of my thought process, and hopefully your thought process as well.

All in all, if you were stuck on a problem that I cover here, I'm confident you'll develop the intuition to solve it yourself after reading my coverage.

What if you (the reader) are better than me?

Then I humbly welcome any feedback you have for these solutions! I can be reached at chat@franklinyin.com. You're also more than welcome to stick along for the ride - my next goal is Guardian!

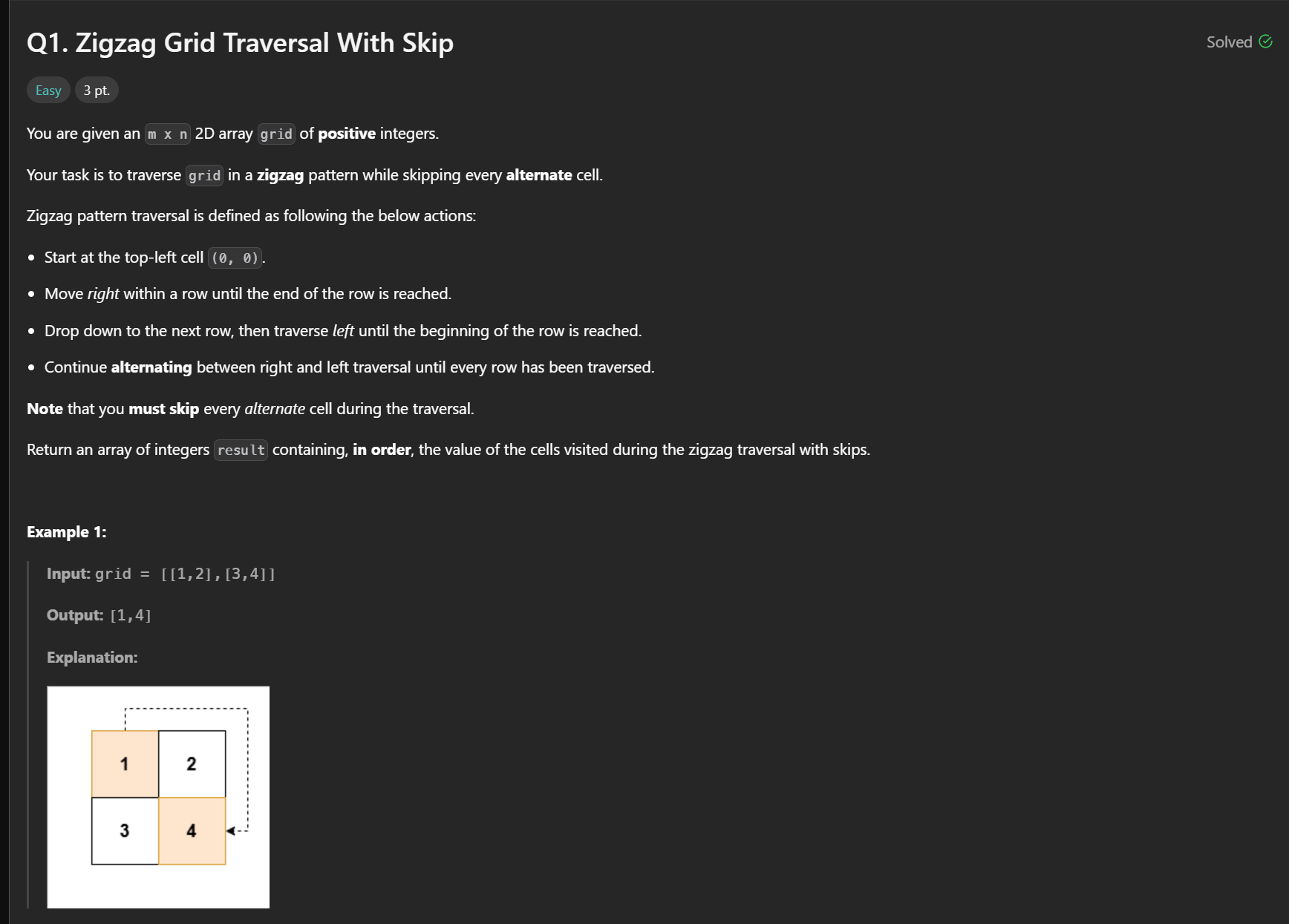
#1 Zigzag Grid Traversal

Constraints

• 2 <= n == grid.length <= 50
• 2 <= m == grid[i].length <= 50
• 1 <= grid[i][j] <= 2500

Intution

For this problem we just need to do exactly what it says - there are no clever tricks, we iterate through the 2D array one row at a time. The only things we need to keep track of are direction (we traverse forwards through the first row, backwards through the second row, forwards through the third row, backwards through the fourth row, ...) and cell count (we visit the first cell, skip the second cell, visit the third cell, skip the fourth cell, ...).

Notice that the direction and cell count patterns repeat on every other turn, kind of like flipping a switch on and off. Two ways to simulate this switching behavior are to multiply a number by negative 1 (the switch is "on" if the number is positive, "off" if negative) or by adding 1 to a number and checking if it's even ("on" if number is even, "off" if number is odd).

Solution

Here's a link to my original submission.

class Solution:
    def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:
        # A
        dir = 1
        count = 0
        ans = []
        # B
        for r in range(len(grid)):
            # C
            iterd = range(len(grid[0])) if dir == 1 else reversed(range(len(grid[0])))
            for c in iterd:
                # D
                if count % 2 == 0:
                    ans.append(grid[r][c])
                # E
                count += 1
            # F
            dir *= -1
        return ans

• A: Variable initialization. dir will represent whether the current row should be read backwards or forwards, count will represent whether we should visit or skip the current cell, and ans will contain our final answer (the collection of all visited cells).
• B: Nested for loop to iterate through the grid. Normally it would look something like this:

for r in range(len(grid)):
    for c in range(len(grid[0])):
        print(grid[r][c])

but since the direction of the inner loop (where we will be traversing the entire row r) needs to alternate, our inner loop will need to look a bit different.

• C: This is our modified inner loop. iterd basically stores the for loop that will be used for this iteration. If dir is positive (switch is "on"), we will go in the forward direction and we use the normal for loop:

for c in range(len(grid[0])):

if dir is negative (switch if "off") we will instead use the reversed for loop:

for c in reversed(range(len(grid[0])))

• D: Remember that we have to skip every other cell. Thus, if count is even (the switch is flipped "on") we will add grid[r][c] to ans. If count is odd we skip grid[r][c] instead.
• E: Either way, we need to remember to increment count by 1 ("flip the switch").
• F: Let's also "flip the switch" for dir - we're going the opposite way now, so multiply dir by -1.

Admittedly, there are many optimizations that can be made to this implementation, but the general principles here are solid. Remember that whenever we need to keep track of alternating states, flipping positive/negative or even/odd are good ways to do so.

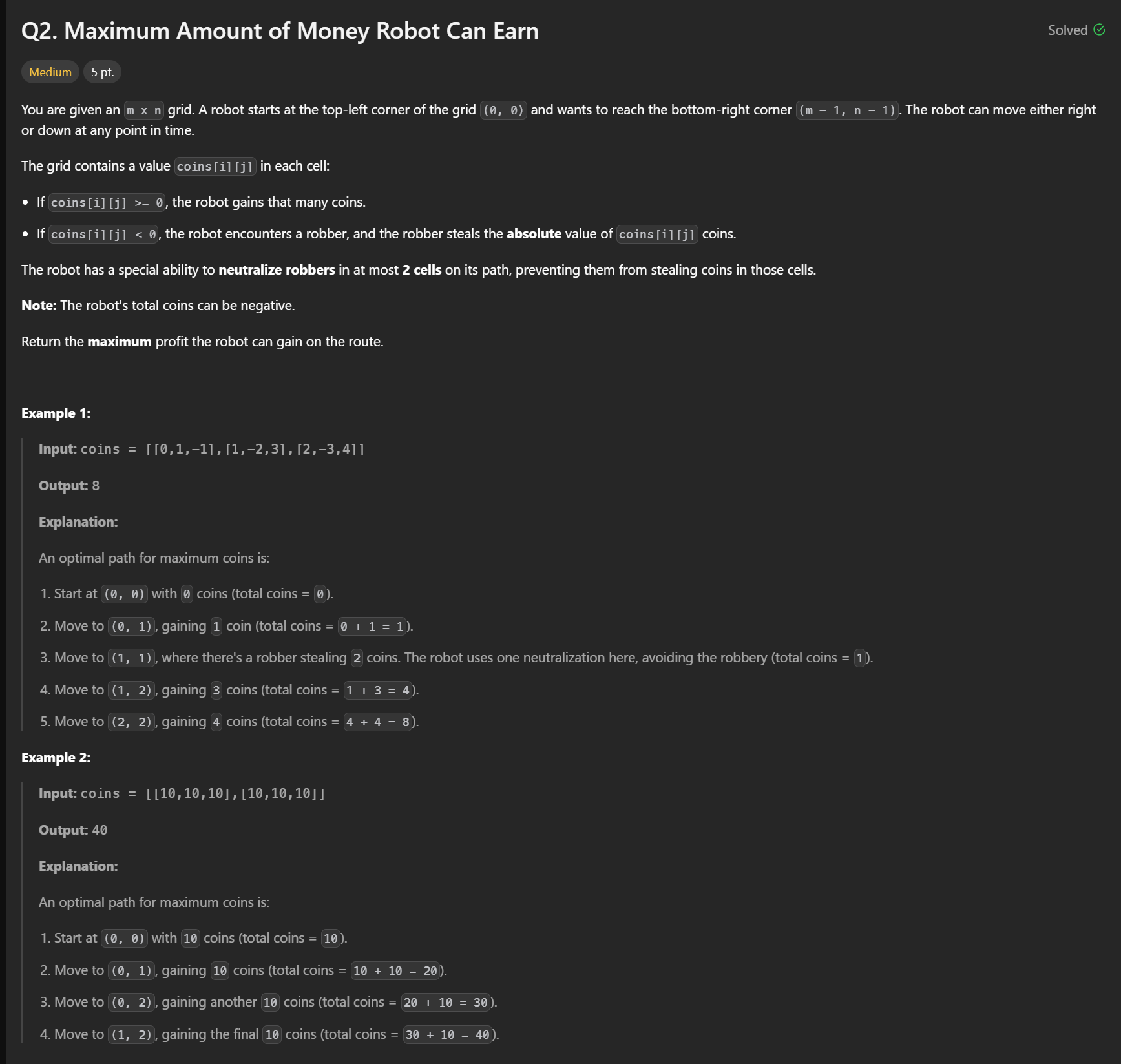
#2 Maximum Amount of Money Robot Can Earn

many billions at least, have you seen veo2?

Constraints

• m == coins.length
• n == coins[i].length
• 1 <= m, n <= 500
• -1000 <= coins[i][j] <= 1000

Intuition

This is a backtracking/dynamic programming problem, so if you're not already familiar with these topics, I recommend you check out a resource like Neetcode's roadmap. That's how I learned these concepts!

I've always thought of DP as a subset of backtracking problems. That is, if the answer to your backtracking problem depends on smaller instances of the same problem, then you can benefit from memoization!

I have a 3-step thought process for solving these problems:

1. Representation - what is the least amount of information, or state, we need to solve this problem? For example, the least amount of state we need to find the Nth finbonacci number is just the number N itself.
2. Implementation - Define a function f that represents the solution to your problem for a given state. Then figure out how f can recursively solve the problem by breaking it into smaller subproblems. For instance, for Fibonacci numbers, the transition is f(N)=f(N−1)+f(N−2). Essentially, this step is about defining how the current state relates to smaller states.
3. Base Case - how can we make sure this function doesn't run forever?

Let's go through these steps now for this problem:

1. Representation: We always need to know where the robot is because that determine what our next possible steps are. Thus, our state at least needs to have the current coordinates (i, j) of the robot. We also need to remember how many more times the robot can use its special ability to neutralize robbers, because if the power is used twice it can no longer be used (changes our decision tree). Lastly, remember that the goal of the question is return the maximum amount of money the robot can collect while traversing the maze. Does this mean we need to keep track of the robot's current value in the state as well? (The answer is no. Can you think of why?)
2. Implementation: We've said that the problem can be represented as dp(i, j, neut) where neut is the number of neutralizations remaining. For each state (i, j, neut) the possible moves are (i+1, j, neut), (i, j+1, neut). If the cell[i][j] has a robber, the moves (i+1, j, neut - 1) and (i, j+1, neut - 1) are also possible.
3. Base Case: We should essentially have two base cases - one where the robot reachs the bottom right corner, and one where it does not but goes out of bounds instead. Think about how these two cases should be handled differently.

Solution

Here's a link to my original submission.

class Solution:
    def maximumAmount(self, coins: List[List[int]]) -> int:
        # A
        self.m = len(coins)
        self.n = len(coins[0])

        # B
        @lru_cache(maxsize=None)
        def dp(i, j, neut):
            # C
            if i >= self.m or j >= self.n:
                return float('-inf')
            if i == self.m - 1 and j == self.n - 1:
                if coins[i][j] < 0 and neut > 0:
                    return 0
                return coins[i][j]

            # D
            modifier = coins[i][j]
            ans = []
            # E
            if modifier < 0 and neut > 0:
                ans.append(dp(i+1, j, neut - 1))
                ans.append(dp(i, j+1, neut - 1))
            # F
            ans.append(dp(i+1, j, neut) + modifier)
            ans.append(dp(i, j+1, neut) + modifier)
            # G
            return max(ans)

        # H    
        return dp(0, 0, 2)

• A: Store the dimensions of the grid (m and n) to simplify boundary checks.
• B: Define a memoized recursive function dp(i, j, neut) . This function computes the maximum coins the robot can collect starting from cell (i, j) with neut remaining neutralizations available. The Python decorator @lru_cache does the memoization for us, it essentially creates a memoization dictionary using the arguemtns of dp() as values. maxsize=None means there is no limit to the size of the cahce.
• C: Base Cases:
  • If the robot steps out of bounds (i >= m or j >= n), return negative infinity (-inf) because it's an invalid state.
  • If the robot reaches the bottom-right cell (m-1, n-1):
    • Check if the cell contains a robber (coins[i][j] < 0) and if neutralizations are available (neut > 0). If so, the robot neutralizes the robber, resulting in 0 coins from this cell.
    • Otherwise, return the value of the cell (coins[i][j]).
• D: Initialize modifier as the value of the current cell (coins[i][j]). This will be added to the robot's total unless it's neutralized. Also initalize ans: this will contain the values of the robot after it takes every possible decision. The idea is to return max(ans) at the end, representing the best possible choice.
• E: If the current cell contains a robber (modifier < 0) and the robot still has neutralizations available (neut > 0), simulate neutralizing the robber. In this case, calculate potential profits from moving right (dp(i, j+1, neut-1)) and moving down (dp(i+1, j, neut-1)) without deducting coins for the robber.
• F: It may be the case that the value at this cell is positive or that we do not want to neutralize this robber. Thus, regardless of whether the robber is neutralized, calculate profits as if we are forced to pick up the value at this cell.
• G: Return the maximum value among all possible moves (max(ans)). This ensures the robot takes the optimal path.
• H: Start the computation from the top-left corner (0, 0) with 2 neutralizations available. The result is the maximum profit the robot can collect.